已知函数f(x)是定义在R上不恒为零的函数,且对于任意实数a,b∈R,满足: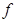 
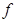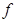(ab)= a(b)+b(a), 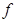(2)="2," an=
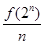(n∈N*), bn=
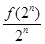(n∈N*).
考察下列结论: ①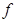(0)= 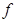(1); ②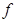(x)为偶函数; ③数列{an}为等比数列; ④数列{bn}为等差数列.其中正确的结论共有( )
| A．1个 | B．2个 | C．3个 | D．4个 |
相关试题
的前n项和为
，已知
，
,则
（）
的图象向右平移
（
轴对称，则
，若
则
的部分图像如右图所示，则在区间
上，下列函数中与
的定义域是
，则函数
的定义域是（）
推荐套卷
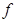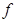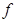已知函数f(x)是定义在R上不恒为零的函数,且对于任意实数a,b∈R,满足: (ab)= a(b)+b(a), 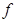(2)="2," an=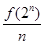(n∈N*), bn=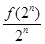(n∈N*).
考察下列结论: ①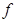(0)= 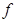(1); ②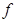(x)为偶函数; ③数列{an}为等比数列; ④数列{bn}为等差数列.其中正确的结论共有( )
| A．1个 | B．2个 | C．3个 | D．4个 |
粤公网安备 44130202000953号