(本小题满分13分)已知椭圆
 (
( )的长轴长为
)的长轴长为 ,且过点
,且过点 .
.
(1)求椭圆 的方程;
的方程;
(2)设 、
、 、
、 是椭圆上的三点,若
是椭圆上的三点,若 ,点
,点 为线段
为线段 的中点,
的中点, 、
、 两点的坐标分别为
两点的坐标分别为 、
、 ,求证:
,求证: .
.
(本大题满分13分)对于给定数列 ,如果存在实常数
,如果存在实常数 使得
使得 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列 是 “线性数列”.
是 “线性数列”.
(1)若 ,
, ,
, ,数列
,数列 、
、 是否为“线性数列”?若是,指出它对应的实常数
是否为“线性数列”?若是,指出它对应的实常数 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列 是“线性数列”,则数列
是“线性数列”,则数列 也是“线性数列”;
也是“线性数列”;
(3)若数列 满足
满足 ,
, ,
, 为常数.求数列
为常数.求数列 前
前 项的和.
项的和.
【原创】已知函数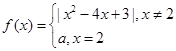 ,若方程
,若方程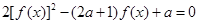 有9个不同的实数解,则实数
有9个不同的实数解,则实数 的取值范围是( )
的取值范围是( )
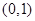 B.
B.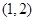 C.
C.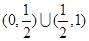 D.
D.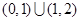
(本小题满分14分)已知函数 ,
,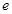 为自然对数的底数.
为自然对数的底数.
(1)过点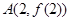 的切线斜率为
的切线斜率为 ,求实数
,求实数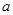 的值;
的值;
(2)当 时,求证:
时,求证: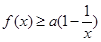 ;
;
(3)在区间 上
上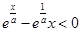 恒成立,求实数
恒成立,求实数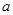 的取值范围.
的取值范围.
(本小题满分12分)如图所示,椭圆 :
: ,其中
,其中 ,焦距为
,焦距为 ,过点
,过点 的直线
的直线 与椭圆
与椭圆 交于点
交于点 、
、 ,点
,点 在
在 之间,又点
之间,又点 ,
, 的中点横坐标为
的中点横坐标为 ,且
,且 .
.
(1)求椭圆 的标准方程 ;
的标准方程 ;
(2)求实数 的值.
的值.
已知双曲线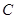 :
: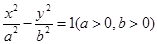 的两条渐近线与抛物线
的两条渐近线与抛物线 的准线分别交于
的准线分别交于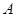 ,
,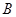 两点,
两点,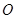 为坐标原点,若双曲线
为坐标原点,若双曲线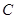 的离心率为2,
的离心率为2,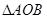 的面积为
的面积为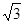 ,则
,则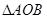 的内切圆半径为( )
的内切圆半径为( )
A.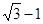 |
B.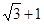 |
C.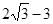 |
D.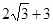 |
(本小题满分12分)某市规定,高中学生三年在校期间参加不少于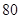 小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段
小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段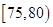 ,
, ,
, ,
,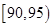 ,
,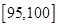 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
(1)求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;
(2)从全市高中学生(人数很多)中任意选取3位学生,记 为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量
为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量 的分布列和数学期望
的分布列和数学期望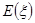 .
.
(本小题满分13分)已知椭圆C: (a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程.
(2)设F为椭圆C的左焦点,T为直线x=-3上任意一点,过F作TF的垂线交椭圆C于点P,Q.
①证明:OT平分线段PQ(其中O为坐标原点);
②当 最小时,求点T的坐标.
最小时,求点T的坐标.
【改编】函数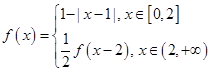 ,则下列命题中正确命题的个数是 ( ).
,则下列命题中正确命题的个数是 ( ).
①函数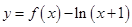 有
有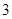 个零点;
个零点;
②若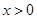 时,函数
时,函数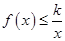 恒成立,则实数
恒成立,则实数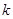 的取值范围是
的取值范围是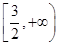 ;
;
③函数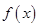 的极大值中一定存在最小值;
的极大值中一定存在最小值;
④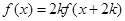
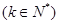 ,对一切
,对一切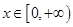 恒成立.
恒成立.
A.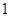 |
B.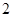 |
C.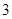 |
D. |
(本小题满分14分)已知函数 ,
, , 其中,
, 其中, 是自然对数的底数.函数
是自然对数的底数.函数 ,
, .
.
(Ⅰ)求 的最小值;
的最小值;
(Ⅱ)将 的全部零点按照从小到大的顺序排成数列
的全部零点按照从小到大的顺序排成数列 ,求证:
,求证:
(1) ,其中
,其中 ;
;
(2) .
.
(本小题满分13分)已知椭圆C: (a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程.
(2)设F为椭圆C的左焦点,T为直线x=-3上任意一点,过F作TF的垂线交椭圆C于点P,Q.
①证明:OT平分线段PQ(其中O为坐标原点);
②当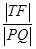 最小时,求点T的坐标.
最小时,求点T的坐标.
(本小题满分12分)已知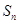 是等差数列
是等差数列 的前n项和,数列
的前n项和,数列 是等比数列,
是等比数列,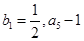 恰为
恰为 的等比中项,圆
的等比中项,圆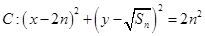 ,直线
,直线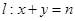 ,对任意
,对任意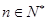 ,直线
,直线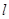 都与圆C相切.
都与圆C相切.
(Ⅰ)求数列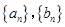 的通项公式;
的通项公式;
(Ⅱ)若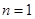 时,
时,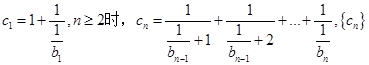 的前n项和为
的前n项和为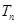 ,求证:对任意
,求证:对任意 ,都有
,都有
已知 ,直线l:y=-2,动点P到直线l的距离为d,且d=
,直线l:y=-2,动点P到直线l的距离为d,且d= .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)直线m:y= 与点P的轨迹交于M、N两点,当
与点P的轨迹交于M、N两点,当 时,求直线m的倾斜角α的取值范围;
时,求直线m的倾斜角α的取值范围;
(Ⅲ)设直线h与点P的轨迹交于C、D两点,写出命题“如果直线h过点B,那么 =-12”的逆命题,并判断该逆命题的真假,请说明理由.
=-12”的逆命题,并判断该逆命题的真假,请说明理由.
设函数 ,数列
,数列 满足
满足
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)记 试比较
试比较 与Q的大小关系,并说明理由.
与Q的大小关系,并说明理由.
(本小题满分14分)已知函数 在
在 点处的切线与直线
点处的切线与直线 垂直,在
垂直,在 处的切线与直线
处的切线与直线 平行.
平行.
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)若 的图象与x轴有且只有3个交点,求b的取值范围.
的图象与x轴有且只有3个交点,求b的取值范围.