在实数集R中,我们定义的大小关系“ ”为全体实数排了一个序,类似地,我们在复数集C上也可以定义一个称为“序”的关系,记为“
”为全体实数排了一个序,类似地,我们在复数集C上也可以定义一个称为“序”的关系,记为“ ”,定义如下:对于任意两个复数
”,定义如下:对于任意两个复数

 ,
, 当且仅当
当且仅当 ,下面命题① 1
,下面命题① 1 i
i 0;②若
0;②若 ,
, ,则
,则 ;③若
;③若 ,则对于任意
,则对于任意 ,
, ;④对于复数
;④对于复数 ,则
,则 其中真命题是
其中真命题是
已知双曲线 的左右焦点分别是
的左右焦点分别是 ,设P是双曲线右支上一点,
,设P是双曲线右支上一点, 在
在 上的投影的大小恰好为
上的投影的大小恰好为 ,且它们的夹角为
,且它们的夹角为 ,则双曲线的渐近线方程为
,则双曲线的渐近线方程为
已知函数 对任意的
对任意的 恒有
恒有 成立.
成立.
(1)当b=0时,记 若
若 在
在 )上为增函数,求c的取值范围;
)上为增函数,求c的取值范围;
(2)证明:当 时,
时, 成立;
成立;
(3)若对满足条件的任意实数b,c,不等式 恒成立,求M的最小值.
恒成立,求M的最小值.
已知数列 的前n项的和为
的前n项的和为 ,且
,且 ,
,
(1)证明数列 是等比数列
是等比数列
(2)求通项 与前n项的和
与前n项的和 ;
;
(3)设 若集合M=
若集合M= 恰有4个元素,求实数
恰有4个元素,求实数 的取值范围.
的取值范围.
已知圆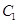 的圆心在坐标原点O,且恰好与直线
的圆心在坐标原点O,且恰好与直线 相切.
相切.
(1)求圆的标准方程;
(2)设点A为圆上一动点,AN
 轴于N,若动点Q满足
轴于N,若动点Q满足 (其中m为非零常数),试求动点
(其中m为非零常数),试求动点 的轨迹方程
的轨迹方程 .
.
(3)在(2)的结论下,当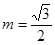 时,得到动点Q的轨迹曲线C,与
时,得到动点Q的轨迹曲线C,与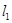 垂直的直线
垂直的直线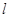 与曲线C交于 B、D两点,求
与曲线C交于 B、D两点,求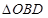 面积的最大值.
面积的最大值.
已知圆O的半径为1,PA,PB为该圆的两条切线,A,B为两切点,那么 的最小值等于.( )
的最小值等于.( )
A. |
B.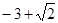 |
C.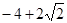 |
D.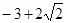 |
在实数集R中,我们定义的大小关系“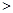 ”为全体实数排了一个序,类似地,我们在复数集C上也可以定义一个称为“序”的关系,记为“
”为全体实数排了一个序,类似地,我们在复数集C上也可以定义一个称为“序”的关系,记为“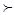 ”,定义如下:对于任意两个复数
”,定义如下:对于任意两个复数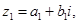

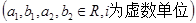 ,
,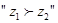 当且仅当
当且仅当 ,下面命题①1
,下面命题①1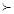 i
i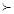 0;②若
0;②若 ,
, ,则
,则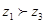 ;③若
;③若 ,则对于任意
,则对于任意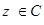 ,
,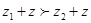 ;④对于复数
;④对于复数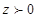 ,则
,则 其中真命题是
其中真命题是
已知双曲线 的左右焦点分别是
的左右焦点分别是 ,设P是双曲线右支上一点,
,设P是双曲线右支上一点, 在
在 上的投影的大小恰好为
上的投影的大小恰好为 ,且它们的夹角为
,且它们的夹角为 ,则双曲线的渐近线方程为
,则双曲线的渐近线方程为
我们把离心率为e=的双曲线 (a>0,b>0)称为黄金双曲线.如图,
(a>0,b>0)称为黄金双曲线.如图, 是双曲线的实轴顶点,
是双曲线的实轴顶点, 是虚轴的顶点,
是虚轴的顶点, 是左右焦点,
是左右焦点, 在双曲线上且过右焦点
在双曲线上且过右焦点 ,并且
,并且 轴,给出以下几个说法:
轴,给出以下几个说法:
①双曲线x2- =1是黄金双曲线;
=1是黄金双曲线;
②若b2=ac,则该双曲线是黄金双曲线;
③如图,若∠F1B1A2=90°,则该双曲线是黄金双曲线;
④如图,若∠MON=90°,则该双曲线是黄金双曲线.
其中正确的是( )
| A.①②④ | B.①②③ | C.②③④ | D.①②③④ |
已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上且过点
轴上且过点 ,离心率是
,离心率是 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)直线过点 且与椭圆
且与椭圆 交于
交于 ,
, 两点,若
两点,若 ,求直线的方程.
,求直线的方程.
平面内与两定点 、
、 (
( )连线的斜率之积等于非零常数m的点的轨迹,加上
)连线的斜率之积等于非零常数m的点的轨迹,加上 、
、 两点所成的曲线C可以是圆、椭圆或双曲线.求曲线C的方程,并讨论C的形状与m值得关系.
两点所成的曲线C可以是圆、椭圆或双曲线.求曲线C的方程,并讨论C的形状与m值得关系.