高中数学试题

已知A={2，3，4}，B={x||x|＜3}，则A∩B=（ ）

A．{3}

B．{2，3}

C．{2}

D．{2，3，4}

设全集U={x∈Z|﹣2＜x＜4}，集合S与T都为U的子集，S∩T={2}，（∁_US）∩T={﹣1}，（∁_US）∩（∁_UT）={1，3}，则下列说法正确的是（ ）

A．0属于S，且0属于T

B．0属于S，且0不属于T

C．0不属于S但0属于T

D．0不属于S，也不属于T

已知函数f（x）=ax²+bx+c，满足f（1）=﹣，且3a＞2c＞2b．
（1）求证：a＞0时，的取值范围；
（2）证明函数f（x）在区间（0，2）内至少有一个零点；
（3）设x₁，x₂是函数f（x）的两个零点，求|x₁﹣x₂|的取值范围．

已知函数f（x）=log₂（m+）（m∈R，且m＞0）．
（1）求函数f（x）的定义域；
（2）若函数f（x）在（4，+∞）上单调递增，求m的取值范围．

已知函数f（x）=lg（x²﹣5x+6）和的定义域分别是集合A、B，
（1）求集合A，B；
（2）求集合A∪B，A∩B．

已知集合A={x|a﹣1＜x＜2a+1}，B={x|0＜x＜1}
（1）若a=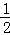，求A∩B．
（2）若A∩B=∅，求实数a的取值范围．

函数f（x）=a^x﹣1+3的图象一定过定点P，则P点的坐标是      ．

U={1，2，3，4}，A={1，2}，B={1，3}，则A∩C_UB为（ ）

A．{1}

B．{2}

C．4

D．{1，2，4}

已知函数f（x）=x²+（2a﹣1）x+b是偶函数，那么函数的定义域为（ ）

A．

B．

C．（0，2]

D．[2，+∞）

函数y=f（x）在[0，2]上单调递增，且函数f（x+2）是偶函数，则下列结论成立的是（ ）

A．f（1）＜f（）＜f（）

B．f（）＜f（1）＜f（）

C．f（）＜f（）＜f（1）

D．f（）＜f（1）＜f（）

函数f（x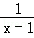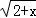）=+的定义域为（ ）

A．[﹣2，+∞）

B．（﹣∞，﹣2]

C．R

D．[﹣2，1）∪（1，+∞）

设偶函数f（x）满足f（x）=2^x﹣4（x≥0），则{x|f（x﹣2）＜0}=（ ）

A．{x|x＜﹣2或x＞4}

B．{x|x＜0或x＞4}

C．{x|x＜0或x＞6}

D．{x|0＜x＜4}

三个数6^0.5，0.5⁶，log_0.56的大小顺序为（ ）

A．log0.56＜0.5^6＜6^0.5	B．log0.56＜6^0.5＜0.5^6
C．0.5^6＜6^0.5＜log0.56	D．0.5^6＜log0.56＜6^0.5

已知集合M={x|x²＜1}，N={x|x＞0}，则M∩N=（ ）

A．∅

B．{x|x＞0}

C．{x|x＜1}

D．{x|0＜x＜1}

已知集合M={x|x＜1}，N={x|2^x＞1}，则M∩N=（ ）

A．∅

B．{x|x＜0}

C．{x|x＜1}

D．{x|0＜x＜1}