甲、乙两个准备在一段长为1200米的笔直公路上进行跑步,甲、乙跑步的速度分别为4 和6
和6 ,起跑前乙在起点,甲在乙前面100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两之间的距离
,起跑前乙在起点,甲在乙前面100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两之间的距离 与时间
与时间 的函数图象是 ( )
的函数图象是 ( )
如图,已知一次函数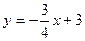 的图象与
的图象与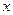 轴,
轴,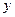 轴分别相交于A,B两点,点C在AB上以每秒1个单位的速度从点B向点A运动,同时点D在线段AO上以同样的速度从点A向点O运动,运动时间用
轴分别相交于A,B两点,点C在AB上以每秒1个单位的速度从点B向点A运动,同时点D在线段AO上以同样的速度从点A向点O运动,运动时间用 (单位:秒)表示.
(单位:秒)表示.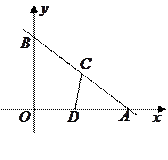
(1)求AB的长;
(2)当 为何值时,△ACD与△ABO相似?并直接写出此时点C的坐标.
为何值时,△ACD与△ABO相似?并直接写出此时点C的坐标.
如图,以Rt△ABO的直角顶点O为原点,OA所在的直线为x轴,OB所在的直线为y轴,建立平面直角坐标系.已知OA=4,OB=3,一动点P从O出发沿OA方向,以每秒1个
单位长度的速度向A点匀速运动,到达A点后立即以原速沿AO返回;点Q从A点出发
沿AB以每秒1个单位长度的速度向点B匀速运动.当Q到达B时,P、Q两点同时停止
运动,设P、Q运动的时间为t秒(t>0).
(1) 试求出△APQ的面积S与运动时间t之间的函数关系式;
(2) 在某一时刻将△APQ沿着PQ翻折,使得点A恰好落在AB边的点D处,如图①.
求出此时△APQ的面积.
(3) 在点P从O向A运动的过程中,在y轴上是否存在着点E使得四边形PQBE为等腰梯
形?若存在,求出点E的坐标;若不存在,请说明理由.
(4) 伴随着P、Q两点的运动,线段PQ的垂直平分线DF交PQ于点D,交折线QB-BO-OP于点F. 当DF经过原点O时,请直接写出t的值.
重庆市垫江县具有2000多年的牡丹种植历史.每年3月下旬至4月上旬,主要分布在该县太平镇、澄溪镇明月山一带的牡丹迎春怒放,美不胜收.由于牡丹之根———丹皮是重要中药材,目前已种植有60多个品种2万余亩牡丹的垫江,因此成为我国丹皮出口基地,获得“丹皮之乡”的美誉。为了提高农户收入,该县决定在现有基础上开荒种植牡丹并实行政府补贴,规定每新种植一亩牡丹一次性补贴农户若干元,经调查,种植亩数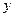 (亩)与补贴数额
(亩)与补贴数额 (元)之间成一次函数关系,且补贴与种植情况如下表:
(元)之间成一次函数关系,且补贴与种植情况如下表:
| 补贴数额(元) |
10 |
20 |
…… |
| 种植亩数(亩) |
160 |
240 |
…… |
随着补贴数额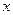 的不断增大,种植规模也不断增加,但每亩牡丹的收益
的不断增大,种植规模也不断增加,但每亩牡丹的收益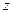 (元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(1)分别求出政府补贴政策实施后,种植亩数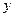 (亩)、每亩牡丹的收益
(亩)、每亩牡丹的收益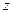 (元)与政府补贴数额
(元)与政府补贴数额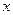 (元)之间的函数关系式;
(元)之间的函数关系式;
(2)要使全县新种植的牡丹总收益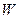 (元)最大,又要从政府的角度出发,政府应将每亩补贴数额
(元)最大,又要从政府的角度出发,政府应将每亩补贴数额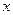 定为多少元?并求出总收益
定为多少元?并求出总收益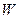 的最大值和此时种植亩数;(总收益=每亩收益×亩数)
的最大值和此时种植亩数;(总收益=每亩收益×亩数)
(3)在(2)问中取得最大总收益的情况下,为了发展旅游业,需占用其中不超过50亩的新种牡丹园,利用其树间空地种植刚由国际牡丹园培育出的“黑桃皇后”.已知引进该新品种平均每亩的费用为530元,此外还要购置其它设备,这项费用(元)等于种植面积(亩)的平方的25倍.这样混种了“黑桃皇后”的这部分土地比原来种植单一品种牡丹时每亩的平均收益增加了2000元,这部分混种土地在扣除所有费用后总收益为85000元.求混种牡丹的土地有多少亩?(结果精确到个位)(参考数据: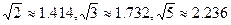 )
)
已知一次函数

①在给定的直角坐标系中作出它的图象;
②此函数图象与x轴、y轴的交点A、B坐标分别为______;______。
③函数图象与坐标轴围成的三角形的周长是多少?
若一次函数y=3x-5与y=2x+7的交点的坐标为(12,31),则方程组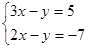 的解为
的解为
已知:一次函数y=4x-3,则该函数图象经过点A(1,__)和B(___,0)
方程组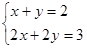 没有解,则此一次函数y=-x+2与y=-x+
没有解,则此一次函数y=-x+2与y=-x+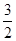 的图象必定
的图象必定
| A.重合 | B.相交 | C.平行 | D.无法判断 |
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为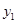 (km),出租车离甲地的距离为
(km),出租车离甲地的距离为 (km),客车行驶时间为
(km),客车行驶时间为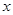 (h),
(h),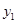 ,
, 与
与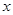 的函数关系图象如图所示:
的函数关系图象如图所示: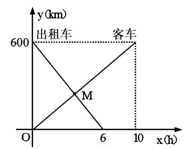
(1)根据图象,求出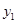 ,
, 关于
关于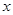 的函数关系式。
的函数关系式。
(2)出发多长时间后两车相遇?此时出租车行驶了多少千米?
生活中,有人喜欢把传送的便条折成 形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为
形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为 ,宽为
,宽为 ,分别回答下列问题:
,分别回答下列问题:
(1)为了保证能折成图④的形状(即纸条两端均超出点 ),试求
),试求 的取值范围.
的取值范围.
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点 的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点
的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点 与点
与点 的距离(用
的距离(用 表示)
表示)