初中数学统计量的选择试题

在数字323233232323323中“3”出现的频率是      ．

如图的两个统计图，女生人数多的学校是（ ）

A．甲校

B．乙校

C．甲、乙两校女生人数一样多

D．无法确定

从全校1200名学生中随机选取一部分学生进行调查，调查情况：A：上网时间小时；B：1小时＜上网时间小时；C：4小时＜上网时间小时；D：上网时间＞7小时．统计结果制成了如
图统计图：

（1）参加调查的学生有  人；
（2）请将条形统计图补全；
（3）请估计全校上网不超过7小时的学生人数．

县医院住院部在连续10天测量某病人的体温与36℃的上下波动数据为：0．2，0．3，0．1，0．1，0，0．2，0．1，0．1，0．1，0，则对这10天中该病人的体温波动数据分析不正确的是（   ）

A．平均数为0．12	B．众数为0．1
C．中位数为0．1	D．方差为0．02

从全校1200名学生中随机选取一部分学生进行调查，调查情况：A：上网时间小时；B：1小时＜上网时间小时；C：4小时＜上网时间小时；D：上网时间＞7小时．统计结果制成了如图统计图：

（1）参加调查的学生有      人；
（2）请将条形统计图补全；
（3）请估计全校上网不超过7小时的学生人数．

已知一组数据x₁，x₂，x₃，x₄，x ₅的方差是，那么另一组数据3x₁-2，3x₂-2，3x₃-2，3x₄-2，3x₅-2的方差是        ．

某校同学参加语文知识竞赛，将学生的成绩，进行整理后分成5组，绘制成频数分布直方图如下，图中从左到右各小组的频率分别是0．0625，0．25，0．375，0．1875，0．125且已知最右边小组的频数为6，结合直方图提供的信息，解答下列问题：

（1）该校参加语文知识竞赛学生共有多少人？
（2）成绩落在哪组数据范围内的人数最多？是多少？
（3）求成绩在80分以下的学生人数．

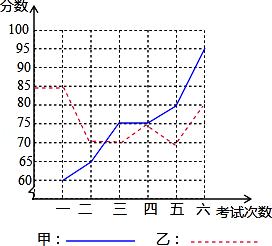
甲、乙两名同学进入初三后，某科6次考试成绩如图：
（1）请根据下图填写如表：

	平均数	方差	中位数	众数	极差
甲	75		75
乙		33．3			15

 
（2）请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行分析：
①从平均数和方差相结合看；
②从折线图上两名同学分数的走势上看，你认为反映出什么问题？

下表给出了某班6名同学身高情况（单位：cm）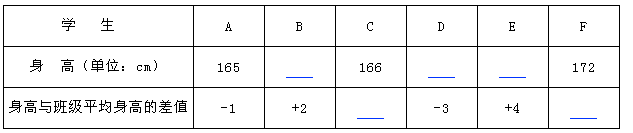

（1）完成表中空的部分；
（2）他们6人中最高身高比最矮身高高多少？
（3）如果身高达到或超过平均身高时叫达标身高，那么这6个同学身高的达标率是多少？（精确到小数点后两位）

某校准备选出甲、乙两人中的一人参加县里的射击比赛，他们在相同条件下各射靶5次，成绩统计如下：

命中环数/环	7	8	9	10
甲命中的频数/次	1	1	0	3
乙命中的频数/次	0	1	3	1

 
（1）求甲、乙两人射击成绩的方差分别是多少？
（2）已知该校选手前三年都取得了县射击比赛的第一名，请问应选择谁去参加比赛？

某水果店一次购进苹果200箱，已经卖出6箱，质量分别是（单位：kg）15．5，16，14．5，13．5，15，15．5．你估计该商店这次进货             kg．

我校男子足球队22名队员的年龄如下表所示：这些队员年龄的众数和中位数分别是（    ）

年龄/岁	14	15	16	17	18	19
人数	2	1	3	6	7	3

A．18，17 B．17，18      C．18，17.5     D．17.5，18

一次期中考试中，甲、乙、丙、丁、戊五位同学的数学、英语成绩等有关信息如下表所示：（单位：分）

	甲	乙	丙	丁	戊	平均分	标准差
数学	71	72	69	68	70
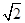英语	88	82	94	85	76	85

 
（1）求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差；
（2）为了比较不同学科考试成绩的好与差，采用标准分是一个合理的选择，标准分的计算公式：
标准分=（个人成绩一平均成绩）÷成绩标准差．
从标准分看，标准分大的考试成绩更好，请问甲同学在本次考试中，数学与英语哪个学科考得更好？

若一组数据a₁，a₂，…，a_n的方差是5，则一组新数据2a₁，…，2a_n的方差是          ．

一组数据23，27，20，18，x，12，它们的中位数是21，则x=           ．