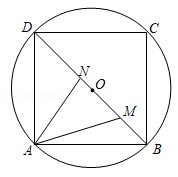
如图,正方形 内接于 ,线段 在对角线 上运动,若 的面积为 , ,则 周长的最小值是
| A. |
3 |
B. |
4 |
C. |
5 |
D. |
6 |
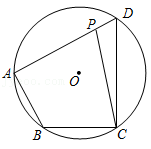
如图,四边形 内接于 ,点 为边 上任意一点(点 不与点 , 重合)连接 .若 ,则 的度数可能为
| A. |
|
B. |
|
C. |
|
D. |
|
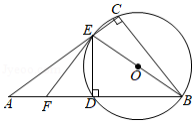
如图,在 中, , 的垂直平分线分别交 、 于点 、 , , 为 的外接圆,过点 作 的切线 交 于点 ,则下列结论正确的是 (写出所有正确结论的序号)
① ;
② ;
③若 ,则 的长为 ;
④ ;
⑤若 ,则 .
以下说法错误的是
| A. |
多边形的内角大于任何一个外角 |
| B. |
任意多边形的外角和是 |
| C. |
正六边形是中心对称图形 |
| D. |
圆内接四边形的对角互补 |
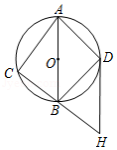
如图,四边形 是 的内接四边形, 是 的直径,连接 .若 ,则 的度数是

| A. |
|
B. |
|
C. |
|
D. |
|
如图.在边长为6的正方形 中,点 , 分别在 , 上, 且 , ,垂足为 , 是对角线 的中点,连接 、则 的长为 .

如图, 的外角 的平分线与它的外接圆相交于点 ,连接 , ,过点 作 ,交 于点 .
求证:(1) ;
(2) 为 的切线.

如图,点 在以 为直径的 上,点 是半圆 的中点,连接 , , , .过点 作 交 的延长线于点 .
(1)求证:直线 是 的切线;
(2)若 , ,求 , 的长.
如图,在 中, ,将 沿直线 翻折得到 ,连接 交 于点 . 是线段 上的点,连接 . 是 的外接圆与 的另一个交点,连接 , .
(1)求证: 是直角三角形;
(2)求证: ;
(3)当 , 时,在线段 上存在点 ,使得 和 互相平分,求 的值.

定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.
(1)如图1, 是 中 的遥望角,若 ,请用含 的代数式表示 .
(2)如图2,四边形 内接于 , ,四边形 的外角平分线 交 于点 ,连结 并延长交 的延长线于点 .求证: 是 中 的遥望角.
(3)如图3,在(2)的条件下,连结 , ,若 是 的直径.
①求 的度数;
②若 , ,求 的面积.
