已知四边形 是平行四边形, , 相交于点 ,下列结论错误的是
| A. |
, |
| B. |
当 时,四边形 是菱形 |
| C. |
当 时,四边形 是矩形 |
| D. |
当 且 时,四边形 是正方形 |
已知平行四边形 中,下列条件:① ;② ;③ ;④ 平分 ,其中能说明平行四边形 是矩形的是
| A. |
① |
B. |
② |
C. |
③ |
D. |
④ |
下列说法正确的是( )
| A. |
有两边和一角分别相等的两个三角形全等 |
| B. |
有一组对边平行,且对角线相等的四边形是矩形 |
| C. |
如果一个角的补角等于它本身,那么这个角等于45° |
| D. |
点到直线的距离就是该点到该直线的垂线段的长度 |
顺次连接菱形四边中点得到的四边形是
| A. |
平行四边形 |
B. |
菱形 |
C. |
矩形 |
D. |
正方形 |
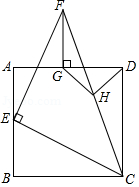
如图,四边形是正方形,
是等腰直角三角形,点
在
上,且
,
,垂足为点
.
(1)试判断与
是否相等?并给出证明;
(2)若点为
的中点,
与
垂直吗?若垂直,给出证明;若不垂直,说明理由.
如图,在中,对角线
与
相交于点
,点
,
分别为
,
的中点,延长
至
,使
,连接
.
(1)求证:;
(2)当与
满足什么数量关系时,四边形
是矩形?请说明理由.

下列判定错误的是
| A. |
平行四边形的对边相等 |
| B. |
对角线相等的四边形是矩形 |
| C. |
对角线互相垂直的平行四边形是菱形 |
| D. |
正方形既是轴对称图形,又是中心对称图形 |
下列命题是真命题的是
| A. |
对角线相等的四边形是矩形 |
| B. |
对角线互相垂直的四边形是矩形 |
| C. |
对角线互相垂直的矩形是正方形 |
| D. |
四边相等的平行四边形是正方形 |
下列命题正确的是
| A. |
有一个角是直角的平行四边形是矩形 |
| B. |
四条边相等的四边形是矩形 |
| C. |
有一组邻边相等的平行四边形是矩形 |
| D. |
对角线相等的四边形是矩形 |
综合与实践
动手操作:
第一步:如图1,正方形纸片沿对角线
所在的直线折叠,展开铺平.在沿过点
的直线折叠,使点
,点
都落在对角线
上.此时,点
与点
重合,记为点
,且点
,点
,点
三点在同一条直线上,折痕分别为
,
.如图2.
第二步:再沿所在的直线折叠,
与
重合,得到图3.
第三步:在图3的基础上继续折叠,使点与点
重合,如图4,展开铺平,连接
,
,
,
.如图5,图中的虚线为折痕.
问题解决:
(1)在图5中,的度数是 ,
的值是 .
(2)在图5中,请判断四边形的形状,并说明理由;
(3)在不增加字母的条件下,请你以图中5中的字母表示的点为顶点,动手画出一个菱形(正方形除外),并写出这个菱形: .

综合与实践
问题情境
在综合与实践课上,老师让同学们以"菱形纸片的剪拼"为主题开展数学活动,如图1,将一张菱形纸片 沿对角线 剪开,得到 和 .
操作发现
(1)将图1中的 以 为旋转中心,按逆时针方向旋转角 ,使 ,得到如图2所示的△ ,分别延长 和 交于点 ,则四边形 的形状是 ;
(2)创新小组将图1中的 以 为旋转中心,按逆时针方向旋转角 ,使 ,得到如图3所示的△ ,连接 , ,得到四边形 ,发现它是矩形,请你证明这个结论;
实践探究
(3)缜密小组在创新小组发现结论的基础上,量得图3中 , ,然后提出一个问题:将△ 沿着射线 方向平移 ,得到△ ,连接 , ,使四边形 恰好为正方形,求 的值,请你解答此问题;
(4)请你参照以上操作,将图1中的 在同一平面内进行一次平移,得到△ ,在图4中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.

已知平行四边形 , 、 是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是
| A. |
|
B. |
|
C. |
|
D. |
|