初中数学矩形的判定试题

问题发现

（1）如图（1），四边形 $\mathit{ABCD}$ 中，若 $\mathit{AB}=\mathit{AD}$ ， $\mathit{CB}=\mathit{CD}$ ，则线段 $\mathit{BD}$ ， $\mathit{AC}$ 的位置关系为 　 　；

拓展探究

（2）如图（2），在 $\text{Rt}\Delta \text{ABC}$ 中，点 $F$ 为斜边 $\mathit{BC}$ 的中点，分别以 $\mathit{AB}$ ， $\mathit{AC}$ 为底边，在 $\text{Rt}\Delta \text{ABC}$ 外部作等腰三角形 $\mathit{ABD}$ 和等腰三角形 $\mathit{ACE}$ ，连接 $\mathit{FD}$ ， $\mathit{FE}$ ，分别交 $\mathit{AB}$ ， $\mathit{AC}$ 于点 $M$ ， $N$ ，试猜想四边形 $\mathit{FMAN}$ 的形状，并说明理由；

解决问题

（3）如图（3），在正方形 $\mathit{ABCD}$ 中， $\mathit{AB}=2\sqrt{2}$ ，以点 $A$ 为旋转中心将正方形 $\mathit{ABCD}$ 旋转 $60°$ ，得到正方形 $\mathit{AB}\text{'}C\text{'}D\text{'}$ ，请直接写出 $\mathit{BD}\text{'}$ 的长度．

如图①，在中，，过上一点作交于点，以为顶点，为一边，作，另一边交于点．

（1）求证：四边形为平行四边形；

（2）当点为中点时，的形状为　　；

（3）延长图①中的到点，使，连接，，，得到图②，若，判断四边形的形状，并说明理由．

如图，菱形的对角线，相交于点，且，．求证：四边形是矩形．

关于 $▱\mathit{ABCD}$ 的叙述，正确的是 $($ 　　 $)$

A．	若 $\mathit{AB}\perp \mathit{BC}$ ，则 $▱\mathit{ABCD}$ 是菱形	B．	若 $\mathit{AC}\perp \mathit{BD}$ ，则 $▱\mathit{ABCD}$ 是正方形
C．	若 $\mathit{AC}=\mathit{BD}$ ，则 $▱\mathit{ABCD}$ 是矩形	D．	若 $\mathit{AB}=\mathit{AD}$ ，则 $▱\mathit{ABCD}$ 是正方形

（年云南省曲靖市）如图，菱形ABCD的对角线AC与BD相交于点O，且BE∥AC，CE∥BD．

（1）求证：四边形OBEC是矩形；
（2）若菱形ABCD的周长是，tanα=，求四边形OBEC的面积．

（年江西省南昌市）（1）如图1，纸片□ABCD中，AD=5，S_□ABCD=15，过点A作AE⊥BC，垂足为E，沿AE剪下△ABE，将它平移至△DCE′ 的位置，拼成四边形AEE′D，则四边形AEE′D的形状为（    ）
A．平行四边形          B．菱形          C．矩形          D．正方形
（2）如图2，在（1）中的四边形纸片AEE′D中，在EE′上取一点F，使EF=4，剪下△AEF，将它平移至△DE′F′ 的位置，拼成四边形AFF′D．
① 求证四边形AFF′D是菱形；
② 求四边形AFF′D两条对角线的长．

如图，在△ABC中，D是BC的中点，E是AD的中点，过点A作AF∥BC，AF与CE的延长线相交于点F，连接BF．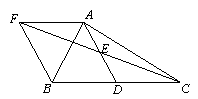

（1）求证：四边形AFBD是平行四边形；
（2）将下列命题填写完整，并使命题成立（图中不再添加其它的点和线）：
①      当△ABC满足条件AB＝AC时，四边形AFBD是        形；
② 当△ABC满足条件                     时，四边形AFBD是正方形．