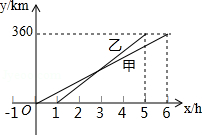
甲、乙两人利用不同的交通工具,沿同一路线从地出发前往
地,甲出发
后,乙出发,设甲与
地相距
,乙与
地相距
,甲离开
地的时间为
,
、
与
之间的函数图象如图所示.
(1)甲的速度是 ;
(2)当时,求
关于
的函数解析式;
(3)当乙与地相距
时,甲与
地相距
.
甲、乙两车分别从、
两地同时出发,甲车匀速前往
地,到达
地立即以另一速度按原路匀速返回到
地;乙车匀速前往
地,设甲、乙两车距
地的路程为
(千米),甲车行驶的时间为
(时
,
与
之间的函数图象如图所示.
(1)求甲车从地到达
地的行驶时间;
(2)求甲车返回时与
之间的函数关系式,并写出自变量
的取值范围;
(3)求乙车到达地时甲车距
地的路程.
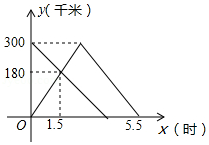
长为的春游队伍,以
的速度向东行进,如图1和图2,当队伍排尾行进到位置
时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为
,当甲返回排尾后,他及队伍均停止行进.设排尾从位置
开始行进的时间为
,排头与
的距离为
.

(1)当时,解答:
①求与
的函数关系式(不写
的取值范围);
②当甲赶到排头位置时,求的值;在甲从排头返回到排尾过程中,设甲与位置
的距离为
,求
与
的函数关系式(不写
的取值范围)
(2)设甲这次往返队伍的总时间为,求
与
的函数关系式(不写
的取值范围),并写出队伍在此过程中行进的路程.
某厂按用户的月需求量(件
完成一种产品的生产,其中
,每件的售价为18万元,每件的成本
(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量
(件
成反比,经市场调研发现,月需求量
与月份
为整数,
,符合关系式
为常数),且得到了表中的数据.
月份 |
1 |
2 |
成本 |
11 |
12 |
需求量 |
120 |
100 |
(1)求与
满足的关系式,请说明一件产品的利润能否是12万元;
(2)求,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第个月和第
个月的利润相差最大,求
.
在平面直角坐标系中的点
和图形
,给出如下的定义:若在图形
上存在一点
,使得
、
两点间的距离小于或等于1,则称
为图形
的关联点.
(1)当的半径为2时,
①在点,
,
,
,
,
中,
的关联点是 .
②点在直线
上,若
为
的关联点,求点
的横坐标的取值范围.
(2)的圆心在
轴上,半径为2,直线
与
轴、
轴交于点
、
.若线段
上的所有点都是
的关联点,直接写出圆心
的横坐标的取值范围.
某商店通过调低价格的方式促销 个不同的玩具,调整后的单价 (元 与调整前的单价 (元 满足一次函数关系,如表:
| |
第1个 |
第2个 |
第3个 |
第4个 |
|
第 个 |
| 调整前的单价 (元 |
|
|
|
|
|
|
| 调整后的单价 (元 |
|
|
|
|
|
|
已知这 个玩具调整后的单价都大于2元.
(1)求 与 的函数关系式,并确定 的取值范围;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?
(3)这 个玩具调整前、后的平均单价分别为 , ,猜想 与 的关系式,并写出推导过程.
某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量(千克)与每千克售价
(元
满足一次函数关系,部分数据如下表:
售价 |
50 |
60 |
70 |
销售量 |
100 |
80 |
60 |
(1)求与
之间的函数表达式;
(2)设商品每天的总利润为(元
,求
与
之间的函数表达式(利润
收入
成本);
(3)试说明(2)中总利润随售价
的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
有一个装有水的容器,如图所示,容器内的水面高度是 ,现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒 的速度匀速增加,则容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是

| A. |
正比例函数关系 |
B. |
一次函数关系 |
| C. |
二次函数关系 |
D. |
反比例函数关系 |
为奖励“我的中国梦”暑期系列实践活动的获奖学生,学校准备在某商店购买A,B两种文具作为奖品,已知一件A种文具的单价比B种文具的单价便宜4元,而用300元买A种文具的件数是用200元买B种文具的件数的2倍.
(1)求A种文具的单价;
(2)根据需要,学校准备在该商店购买A,B两种文具共200件,其中A种文具的件数不多于B种文具件数的3倍.为了节约经费,应购买A,B两种文具各多少件?
有一进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量有两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.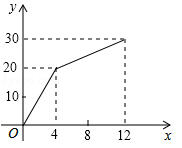
(1)当4≤x≤12时,求y关于x的函数解析式;
(2)直接写出每分进水,出水各多少升.
甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行.乙车出发2h休息.与甲车相遇.继续行驶.设甲、乙两车与B地的距离y(km)与行驶的时间x(h)之间的函数图象如图所示.

(1)写出甲车与B地的距离y(km)与行驶时间x(h)之间的函数关系式 ;
(2)乙车休息的时间为 ;
(3)写出休息前,乙车与B地的距离y(km)与行驶的时间x(h)之间的函数关系式 ;休息后,乙车与B地的距离y(km)与行驶的时间x(h)之间的函数关系式 ;
(4)求行驶多长时间两车相距100km.
设min{x,y}表示x,y两个数中的最小值,例如min{0,2}=0,min{12,8}=8,则关于x的函数y=min{2x,x+2}可以表示为________________.
某居民统计了家里的用水量x(立方米)与应缴水费w(元)之间的关系如下表所示.
(1)写出用水量x(立方米)与水费w(元)之间的关系式.
(2)计算用水量是35立方米时的水费是多少元?