现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是 的正方形,其中一个的某顶点恰好是另一个的中心,则这两个正方形重叠部分的面积恒为
的正方形,其中一个的某顶点恰好是另一个的中心,则这两个正方形重叠部分的面积恒为 .类比到空间,有两个棱长均为
.类比到空间,有两个棱长均为 的正方体,若其中一个的某顶点恰好是另一个的中心,则这两个正方体重叠部分的体积恒为 .
的正方体,若其中一个的某顶点恰好是另一个的中心,则这两个正方体重叠部分的体积恒为 .
已知底面半径为 ,高为
,高为 的圆锥,过高的三等分点作平行于底面的两截面,它们把圆锥侧面分成的三部分的面积之比为()
的圆锥,过高的三等分点作平行于底面的两截面,它们把圆锥侧面分成的三部分的面积之比为()
A. |
B. |
C. |
D. |
如图所示,四边形ABCD为直角梯形, ,
, ,
, 为等边三角形,且平面
为等边三角形,且平面 平面ABE,
平面ABE, ,P为CE中点.
,P为CE中点.
(1)求证: ;
;
(2)求三棱锥D-ABP的体积.
如图所示,四边形ABCD为直角梯形,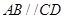 ,
,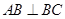 ,
,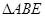 为等边三角形,且平面
为等边三角形,且平面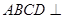 平面ABE,
平面ABE,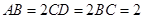 ,P为CE中点.
,P为CE中点.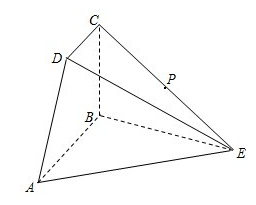
(1)求证: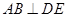 ;
;
(2)求三棱锥D-ABP的体积.
已知某几何体的三视图如图,其中正(主)视图中半圆的半径为1,则该几何体的体积为()
A.24﹣ |
B.24﹣ |
C.24﹣π | D.24﹣ |