现有一个关于平面图形的命题：如图，同一个平面内有两个边长都是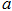
的正方形，其中一个的某顶点恰好是另一个的中心，则这两个正方形重叠部分的面积恒为
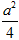．类比到空间，有两个棱长均为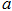的正方体，若其中一个的某顶点恰好是另一个的中心，则这两个正方体重叠部分的体积恒为 ．
，则
的最小值是 ．
的不等式
的解集为
，且
，则实数
的取值范围是 ．
与它的高
的关系是：
，把这个结论推广到空间正四面体，则正四面体内切球的半径
依它的前10项的规律，则
_． 
的展开式的常数项是_________．相关知识点
推荐套卷
现有一个关于平面图形的命题：如图，同一个平面内有两个边长都是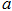的正方形，其中一个的某顶点恰好是另一个的中心，则这两个正方形重叠部分的面积恒为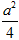．类比到空间，有两个棱长均为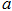的正方体，若其中一个的某顶点恰好是另一个的中心，则这两个正方体重叠部分的体积恒为 ．
粤公网安备 44130202000953号