为了解学生对网上在线学习效果的满意度，某校设置了：非常满意、满意、基本满意、不满意四个选项，随机抽查了部分学生，要求每名学生都只选其中的一项，并将抽查结果绘制成如图统计图（不完整）．
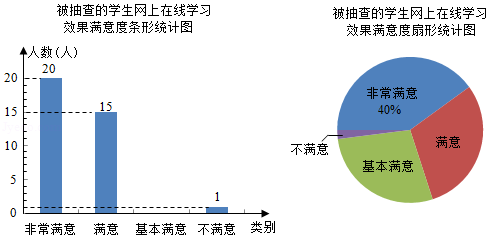
请根据图中信息答案下列问题：
（1）求被抽查的学生人数，并补全条形统计图；（温馨提示：请画在答题卷相对应的图上）
（2）求扇形统计图中表示“满意”的扇形的圆心角度数；
（3）若该校共有1000名学生参与网上在线学习，根据抽查结果，试估计该校对学习效果的满意度是“非常满意”或“满意”的学生共有多少人？
（本题12分） 某公司投资1200万元购买了一条新生产线生产新产品．根据市场调研，生产每件产品需要成本50元，该产品进入市场后不得低于80元/件且不得超过160元/件，该产品销售量y（万件）与产品售价x（元）之间的关系如图所示．
（1）求y与x之间的函数关系式，并写出x的取值范围；
（2）第一年公司是盈利还是亏损？求出当盈利最大或亏损最小时的产品售价；
（3）在（2）的前提下，即在第一年盈利最大或者亏损最小时，公司第二年重新确定产品售价，能否使
前两年盈利总额达790万元？若能，求出第二年产品售价；若不能，说明理由．
（本题10分）如图，从城市A到B城市的公路需经过城市C，图中AC=100千米，∠CAB=25°，∠CBA=37°，因城市规划的需要，将在A、B两城市间修建一条笔直的公路．
（1）求改直的公路AB的长；
（2）问公路改直后比原来缩短了多少千米？
（参考数据：sin25°≈0．42，cos25°≈0．91，sin37°≈0．60，tan37°≈0．75）
（本题10分）如图，在⊙O中，AB为直径，AC为弦，过点C作CD⊥AB于点D，将△ACD沿AC翻折，点D落在点E处，AE交⊙O于点F ,连接OC、FC．
（1）求证：CE是⊙O的切线．
（2）若FC∥AB，求证：四边形 AOCF是菱形．
和△
中，
，
，
，点
在
上．
≌△
；
．
粤公网安备 44130202000953号