若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
(1)已知 是比例三角形, , ,请直接写出所有满足条件的 的长;
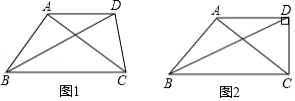
(2)如图1,在四边形 中, ,对角线 平分 , .求证: 是比例三角形.
(3)如图2,在(2)的条件下,当 时,求 的值.
相关知识点
推荐套卷
若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.

(1)已知 是比例三角形, , ,请直接写出所有满足条件的 的长;
(2)如图1,在四边形 中, ,对角线 平分 , .求证: 是比例三角形.
(3)如图2,在(2)的条件下,当 时,求 的值.