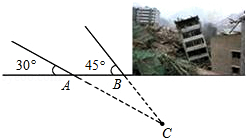
如图,某煤矿因不按规定操作发生瓦斯爆炸,救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面 , 两个探测点探测到地下 处有生命迹象.已知 , 两点相距8米,探测线与地面的夹角分别是 和 ,试确定生命所在点 的深度(结果保留根号).
相关知识点
推荐套卷
如图,某煤矿因不按规定操作发生瓦斯爆炸,救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面 , 两个探测点探测到地下 处有生命迹象.已知 , 两点相距8米,探测线与地面的夹角分别是 和 ,试确定生命所在点 的深度(结果保留根号).
