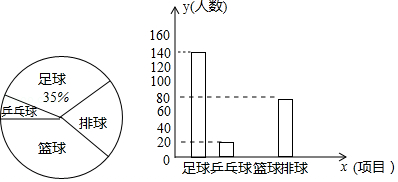
某校为提高学生身体素质，决定开展足球、篮球、排球、乒乓球四项

首页 / 初中数学 / 试题详细

某校为提高学生身体素质，决定开展足球、篮球、排球、乒乓球四项课外体育活动，并要求学生必须并且只能选择一项．为了解选择各种体育活动项目的学生人数，随机抽取了部分学生进行调查，并绘制出以下两幅不完整的统计图．请根据统计图回答下列问题．（要求写出简要的解答过程）

（1）这次活动一共调查了多少名学生？

（2）补全条形统计图．

（3）若该学校总人数是1300人，请估计选择篮球项目的学生人数．

登录免费查看答案和解析

相关试题

（本题7分）如图所示，用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,
其中，GH="2cm," GK="2cm," 设BF=xcm,

（1）用含x的代数式表示CM=cm, DM=cm．
（2）求长方形ABCD的面积．

收藏答案/解析

（本题7分）某自行车厂一周计划生产2100辆电动车，平均每天生产电动车300辆，由于各种原因，实际每天生产量与计划每天生产量相比有出入。下表是某周的生产情况（超产记为正、减产记为负，单位：辆）：

星期	一	二	三	四	五	六	日
减增	+8	-2	-6	+11	-12	+6	+7

（1）根据记录的数据可知，该厂星期一生产电动车辆
（2）产量最多的一天比产量最少的一天多生产电动车辆
（3）该厂实行记件工资制，每生产一辆车可得60元，若超额完成任务，则超额部分每辆车另奖10元，每少生产一辆扣10元，那么该厂工人这一周的工资总额是多少元？

收藏答案/解析

（本题满分10分，每小题5分）先化简，后求值：
（1）5（3x²y－xy²）－3（－xy²＋4x²y），其中x＝1，y＝－．
（2）, 其中=2014．

收藏答案/解析

（本题4分）把下列各数-1²，，，+（+2），在数轴上表示出来，并用“＞”把他们连接起来．

收藏答案/解析

（本题4分）把下列各数填入表示它所在的数集的大括号：
－2．4，3，2．008，－，1，－，0，－（－2．28），π，－|－4|
正数集合：{…}；
负有理数集合：{…}；
整数集合：{…}；
负分数集合：{…}．

收藏答案/解析