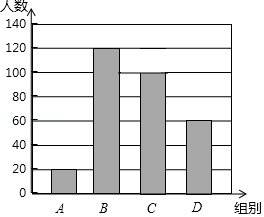
国家规定,中、小学生每天在校体育活动时间不低于 .为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中 组为 , 组为 , 组为 , 组为 .
请根据上述信息解答下列问题:
(1)本次调查数据的中位数落在 组内;
(2)该辖区约有18000名初中学生,请你估计其中达到国家规定体育活动时间的人数.
相关知识点
推荐套卷
国家规定,中、小学生每天在校体育活动时间不低于 .为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中 组为 , 组为 , 组为 , 组为 .
请根据上述信息解答下列问题:
(1)本次调查数据的中位数落在 组内;
(2)该辖区约有18000名初中学生,请你估计其中达到国家规定体育活动时间的人数.
