为了落实党的“精准扶贫”政策, 、 两城决定向 、 两乡运送肥料以支持农村生产,已知 、 两城共有肥料500吨,其中 城肥料比 城少100吨,从 城往 、 两乡运肥料的费用分别为20元 吨和25元 吨;从 城往 、 两乡运肥料的费用分别为15元 吨和24元 吨.现 乡需要肥料240吨, 乡需要肥料260吨.
(1) 城和 城各有多少吨肥料?
(2)设从 城运往 乡肥料 吨,总运费为 元,求出最少总运费.
(3)由于更换车型,使 城运往 乡的运费每吨减少 元,这时怎样调运才能使总运费最少?
相关知识点
推荐套卷
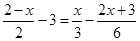
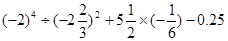
 ,请用
,请用
 粤公网安备 44130202000953号
粤公网安备 44130202000953号