某运动员在一场篮球比赛中的技术统计如表所示：
技术 |
上场时间（分钟） |
出手投篮（次） |
投中 （次） |
罚球得分 |
篮板 （个） |
助攻（次） |
个人总得分 |
数据 |
46 |
66 |
22 |
10 |
11 |
8 |
60 |
注：表中出手投篮次数和投中次数均不包括罚球．
根据以上信息，求本场比赛中该运动员投中2分球和3分球各几个．
相关试题
在△ABC中，P是BC边上的一个动点，以AP为直径的⊙O分别交AB、AC于点E和点F．
（1）若∠BAC＝45°，EF＝4，则AP的长为多少？
（2）在（1）条件下，求阴影部分面积．
（3）试探究：当点P在何处时，EF最短？请直接写出你所发现的结论，不必证明．
如图，AB是⊙O的直径，C是⊙O上一点，AC平分∠BAD；AD⊥ CD，垂足为D．
(1)求证：CD是⊙O的切线
(2)若⊙O的直径为5，CD＝2．求AC的长．
+（1-
）0-（
）-2+︱tan45°-1︱相关知识点
推荐套卷
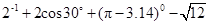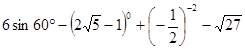
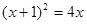
粤公网安备 44130202000953号