在平面直角坐标系中, , , 三点坐标分别为 , , .
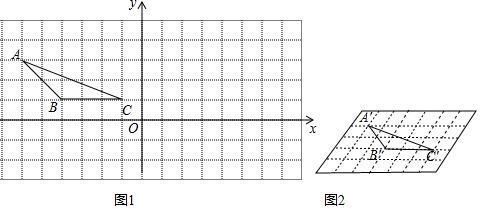
(1)如图1,顺次连接 , , ,得 .
①点 关于 轴的对称点 的坐标是 ,点 关于 轴的对称点 的坐标是 ;
②画出 关于原点对称的△ ;
③ ;
(2)利用四边形的不稳定性,将第二象限部分由小正方形组成的网格,变化为如图2所示的由小菱形组成的网格,每个小菱形的边长仍为1个单位长度,且较小内角为 ,原来的格点 , , 分别对应新网格中的格点 , , ,顺次连接 , , ,得△ ,则 .
相关知识点
推荐套卷
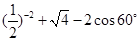 ;
;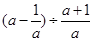 ,其中
,其中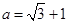 .
.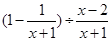 ,从﹣1,2,3中选择一个适当的数作为x值代入.
,从﹣1,2,3中选择一个适当的数作为x值代入.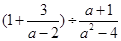 ,其中
,其中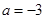 .
.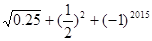 .
.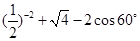 ;
; ,其中
,其中 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号