如图,在平面直角坐标系中,抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,抛物线经过点 和点 ,点 是第一象限抛物线上的一个动点.
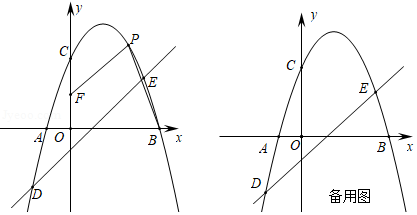
(1)求直线 和抛物线的表达式;
(2)在 轴上取点 ,连接 , ,当四边形 的面积是7时,求点 的坐标;
(3)在(2)的条件下,当点 在抛物线对称轴的右侧时,直线 上存在两点 , (点 在点 的上方),且 ,动点 从点 出发,沿 的路线运动到终点 ,当点 的运动路程最短时,请直接写出此时点 的坐标.
相关知识点
推荐套卷

 。于是,小明以80米/分的速度返回,小明爸爸立
。于是,小明以80米/分的速度返回,小明爸爸立 了几分钟?
了几分钟? 发才不会迟到?(精确到分钟)
发才不会迟到?(精确到分钟)
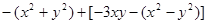 ,其中x= -1,y=2
,其中x= -1,y=2 粤公网安备 44130202000953号
粤公网安备 44130202000953号