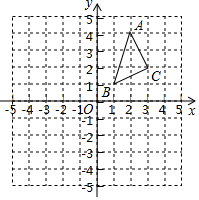
如图, 的三个顶点的坐标分别是 , , .
(1)作出 向左平移4个单位长度后得到的△ ,并写出点 的坐标.
(2)已知△ 与 关于直线 对称,若点 的坐标为 ,请直接写出直线 的函数解析式.
注:点 , , 及点 , , 分别是点 , , 按题中要求变换后对应得到的点.
推荐套卷
如图, 的三个顶点的坐标分别是 , , .
(1)作出 向左平移4个单位长度后得到的△ ,并写出点 的坐标.
(2)已知△ 与 关于直线 对称,若点 的坐标为 ,请直接写出直线 的函数解析式.
注:点 , , 及点 , , 分别是点 , , 按题中要求变换后对应得到的点.
