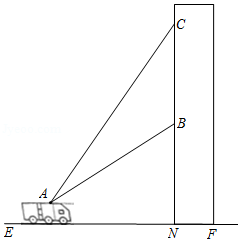
如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点 处的求救者后,又发现点 正上方点 处还有一名求救者,在消防车上点 处测得点 和点 的仰角分别为 和 ,点 距地面2.5米,点 距地面10.5米,为救出点 处的求救者,云梯需要继续上升的高度 约为多少米?
(结果保留整数,参考数据: , , ,
相关知识点
推荐套卷
如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点 处的求救者后,又发现点 正上方点 处还有一名求救者,在消防车上点 处测得点 和点 的仰角分别为 和 ,点 距地面2.5米,点 距地面10.5米,为救出点 处的求救者,云梯需要继续上升的高度 约为多少米?
(结果保留整数,参考数据: , , ,
