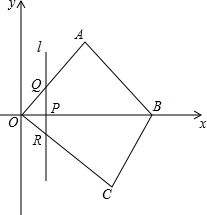
如图，在平面直角坐标系中，四边形OABC的顶点O是坐标原点，点A在第一象限，点C在第四象限，点B在x轴的正半轴上． 且 ，OB，OC的长分别是一元二次方程 的两个根 ．
（1）求点A和点B的坐标．
（2）点P是线段OB上的一个动点（点P不与点O，B重合），过点P的直线l与y轴平行，直线l交边OA或边AB于点Q，交边OC或边BC于点R．设点P的横坐标为t，线段QR的长度为m．已知 时，直线l恰好过点C．当 时，求m关于t的函数关系式．
（3）当 时，请直接写出点P的坐标．
.已知关于x的方程
（1）求证：不论k取什么实数值，这个方程总有实数根；
（2）若等腰三角形ABC的一边长
，另两边的长b，c恰好是这个方程的两根，求△ABC的周长。
. 阅读材料：
小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3+2
=（1+）
，善于思考的小明进行了以下探索：
设a+b=（m+n）（其中a、b、m、n均为正整数）,则有a+b=m2+2n2+2mn,
∴a= m2+2n2,b=2mn.这样小明就找到了一种把部分a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题：
（1）当a、b、m、n均为正整数时，若a+b
=（m+n）,用含m、n的式子分别表示a、b，得：a=，b= ；
（2）利用所探索的结论，找一组正整数a、b、m、n填空：+
=（＋ ）；
（3）若a+4=（m+n），且a、m、n均为正整数，求a的值.
，其中x是一元二次方程
的正数根.A，B两地间的距离为15千米，甲从A地出发步行前往B地，20分钟后，乙从B地出发骑车前往A地，且乙骑车比甲步行每小时多走10千米。乙到达A地后停留40分钟，然后骑车按原路原速返回，结果甲、乙两人同时到达B地。请你就“甲从A地到B地步行所用时间”或“甲步行的速度”提出一个用分式方程解决的问题，并写出解题过程。
≠
（公式法）
粤公网安备 44130202000953号