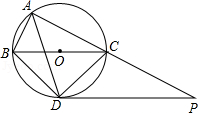
如图，⊙ O是△ ABC的外接圆，点 O在 BC边上，∠ BAC的平分线交⊙ O于点 D，连接 BD、 CD，过点 D作 BC的平行线与 AC的延长线相交于点 P．
（1）求证： PD是⊙ O的切线；
（2）求证：△ ABD∽△ DCP；
（3）当 AB＝5 cm， AC＝12 cm时，求线段 PC的长．
=
，且2a－b+3c=21，试求a∶b∶c.
，求线段PQ的长.相关知识点
推荐套卷
如图，⊙ O是△ ABC的外接圆，点 O在 BC边上，∠ BAC的平分线交⊙ O于点 D，连接 BD、 CD，过点 D作 BC的平行线与 AC的延长线相交于点 P．
（1）求证： PD是⊙ O的切线；
（2）求证：△ ABD∽△ DCP；
（3）当 AB＝5 cm， AC＝12 cm时，求线段 PC的长．
粤公网安备 44130202000953号