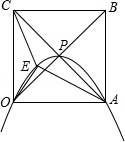
正方形OABC的边长为4，对角线相交于点P，抛物线L经过O、P、A三点，点E是正方形内的抛物线上的动点．
（1）建立适当的平面直角坐标系，
①直接写出O、P、A三点坐标；
②求抛物线L的解析式；
（2）求△OAE与△OCE面积之和的最大值．
=3的解为x=1，求a的值．
-
=3，求
的值．
……
.相关知识点
推荐套卷
正方形OABC的边长为4，对角线相交于点P，抛物线L经过O、P、A三点，点E是正方形内的抛物线上的动点．
（1）建立适当的平面直角坐标系，
①直接写出O、P、A三点坐标；
②求抛物线L的解析式；
（2）求△OAE与△OCE面积之和的最大值．
粤公网安备 44130202000953号