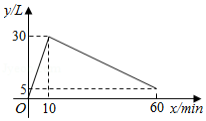
某种机器工作前先将空油箱加满，然后停止加油立即开始工作．当停

首页 / 初中数学 / 试题详细

某种机器工作前先将空油箱加满，然后停止加油立即开始工作．当停止工作时，油箱中油量为 $5 L$ ，在整个过程中，油箱里的油量 $y$ （单位： $L)$ 与时间 $x$ （单位： $\min)$ 之间的关系如图所示．

（1）机器每分钟加油量为　　 $L$ ，机器工作的过程中每分钟耗油量为　　 $L$ ．

（2）求机器工作时 $y$ 关于 $x$ 的函数解析式，并写出自变量 $x$ 的取值范围．

（3）直接写出油箱中油量为油箱容积的一半时 $x$ 的值．

登录免费查看答案和解析

相关试题

一只小虫从某点P出发，在一条直线上来回爬行，假定把向右爬行的路程记为正数，向左爬行的路程记为负数，则爬行各段路程（单位：厘米）依次为：+5，-3，+10，-8，-6，+12，-10。
（1）通过计算说明小虫是否能回到起点P。
（2）如果小虫爬行的速度为0.5厘米/秒，那么小虫共爬行了多长时间？

收藏答案/解析

（共两个小题，10分）
（1）列示表示比a的3倍大4的数与比a的5倍小3的数，计算这两个数的和；
（2）已知A=2xy－2y²+8x²，B=9x²+3xy－5y²，
求 ①A－B； ②－3A+2B.

收藏答案/解析

（共两个小题，每题5分，共10分）先化简，再求值：
（1）－（a²+2a）+3（a²－3a－），其中a=－2
（2）5x²－[2xy－3（xy+2）+4x²]，其中x=－2，y=

收藏答案/解析

（每小题4分，共24分）
（1）－15－（－8）+（－11）－12
（2）（－）×（）×÷（－）
（3）（－2）²+4×（－3）²－（－4）²÷（－2）
（4）－5m²n+4mn²－2mn+6m²n+3mn
（5）ab－+－（－ab）
（6）4x²－[x－（x－3）+3x²]

收藏答案/解析

如图1，在△OAB中，∠OAB=90°，∠AOB=30°，OB=8．以OB为边，在△OAB外作等边△OBC，D是OB的中点，连接AD并延长交OC于E．

（1）求证：四边形ABCE是平行四边形；
（2）如图2，将图1中的四边形ABCO折叠，使点C与点A重合，折痕为FG，求OG的长．

收藏答案/解析