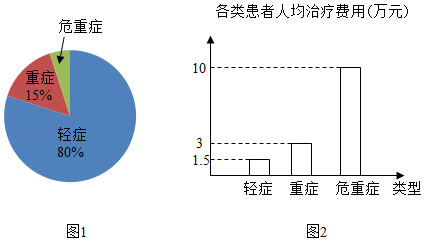
今年 月某市出现了200名新冠肺炎患者，市委根据党中央的决定，对患者进行了免费治疗．图1是该市轻症、重症、危重症三类患者的人数分布统计图（不完整），图2是这三类患者的人均治疗费用统计图．请回答下列问题．
（1）轻症患者的人数是多少？
（2）该市为治疗危重症患者共花费多少万元？
（3）所有患者的平均治疗费用是多少万元？
（4）由于部分轻症患者康复出院，为减少病房拥挤，拟对某病房中的 、 、 、 、 五位患者任选两位转入另一病房，请用树状图法或列表法求出恰好选中 、 两位患者的概率．
相关试题
的绳子剪成两段，并把每一段绳子围成一个正方形.
，该怎么剪？
吗？
中，
，
、
分別是△
；
，试说明四边形
是菱形．
如图，方格纸中有三个点A，B，C，要求作一个四边形使这三个点在这个四边形的边（包括顶点）上，且四边形的顶点在方格的顶点上．
（1）在图甲中作出的四边形是中心对称图形但不是轴对称图形；
（2）在图乙中作出的四边形是轴对称图形但不是中心对称图形；
（3）在图丙中作出的四边形既是轴对称图形又是中心对称图形．
（注：图甲、图乙、图丙在答题纸上）
射击集训队在一个月的集训中，对甲、乙两名运动员进行了10次测试，成绩如图所示（折线图中，粗线表示甲,细线表示乙）：
⑴根据图中所提供的信息填写下表：
⑵如果你是教练，会选择哪位运动员参加比赛？请结合上表中三个统计指标以及折线统计图说明理由。
.推荐套卷
粤公网安备 44130202000953号