某机电厂有甲乙两个发电机生产车间,甲车间每天产量为型发电机和型发电机共45台,其中型发电机数量比型发电机数量多5台.
(1)问甲车间每天生产、两种型号发电机各多少台?
(2)乙车间每天产量为50台,其中型发电机20台,型发电机30台,现有一订单需型发电机720台和型发电机台,但由于受原材料供应限制,两车间不能同时生产,厂里决定由甲乙两车间先后用30天完成订单任务,求甲车间至少需安排生产多少天?由于甲车间还有其他生产任务,最多只能安排27天参加此订单生产,求出所有的可能值.
相关知识点
推荐套卷
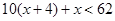 的正整数解是方程
的正整数解是方程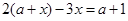 的解,求
的解,求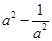 的值。
的值。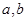 为实数,且
为实数,且 ,求
,求 的平方根。
的平方根。 □ABCD中,
□ABCD中, 于点E,
于点E, 于点F
于点F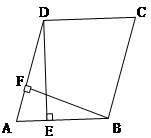


 (5分)
(5分) (5分)
(5分) 粤公网安备 44130202000953号
粤公网安备 44130202000953号