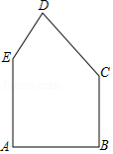
有一块形状如图的五边形余料,,,,,,要在这块余料中截取一块矩形材料,其中一条边在上,并使所截矩形材料的面积尽可能大.
(1)若所截矩形材料的一条边是或,求矩形材料的面积.
(2)能否截出比(1)中更大面积的矩形材料?如果能,求出这些矩形材料面积的最大值;如果不能,说明理由.
推荐套卷
有一块形状如图的五边形余料,,,,,,要在这块余料中截取一块矩形材料,其中一条边在上,并使所截矩形材料的面积尽可能大.
(1)若所截矩形材料的一条边是或,求矩形材料的面积.
(2)能否截出比(1)中更大面积的矩形材料?如果能,求出这些矩形材料面积的最大值;如果不能,说明理由.
