如图，热气球的探测器显示，从热气球A处看一栋高楼顶部B的仰角为30°，看这栋高楼底部C的俯角为65°，热气球与高楼的水平距离AD为120m．求这栋高楼的高度．（结果用含非特殊角的三角函数及根式表示即可）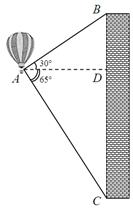
，然后取你喜欢的一组
的值代入求值（提示：所取的值必须使代数式有意义）
，求
的值？
相关知识点
推荐套卷
如图，热气球的探测器显示，从热气球A处看一栋高楼顶部B的仰角为30°，看这栋高楼底部C的俯角为65°，热气球与高楼的水平距离AD为120m．求这栋高楼的高度．（结果用含非特殊角的三角函数及根式表示即可）
粤公网安备 44130202000953号