如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.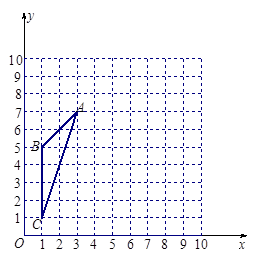
画出将△ABC向右平移3个单位,再向上平移1个单位所得的△A′B′C′;(友情提醒:对应点的字母不要标错!)
建立如图的直角坐标系,请标出△A′B′C′的外接圆的圆心P的位置,并写出圆心P的坐标:P(________);
将△ABC绕BC旋转一周,求所得几何体的全面积.(结果保留π)
相关知识点
推荐套卷
如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.
画出将△ABC向右平移3个单位,再向上平移1个单位所得的△A′B′C′;(友情提醒:对应点的字母不要标错!)
建立如图的直角坐标系,请标出△A′B′C′的外接圆的圆心P的位置,并写出圆心P的坐标:P(________);
将△ABC绕BC旋转一周,求所得几何体的全面积.(结果保留π)