如图13,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离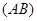 是1.7m,看旗杆顶部
是1.7m,看旗杆顶部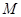 的仰角为
的仰角为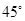 ;小红的眼睛与地面的距离
;小红的眼睛与地面的距离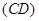 是1.5m,看旗杆顶部
是1.5m,看旗杆顶部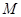 的仰角为
的仰角为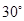 .两人相距28米且位于旗杆两侧(点
.两人相距28米且位于旗杆两侧(点 在同一条直线上).
在同一条直线上).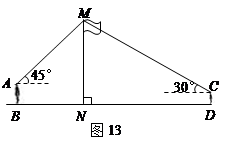
请求出旗杆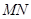 的高度.(参考数据:
的高度.(参考数据: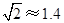 ,
,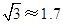 ,结果保留整数)
,结果保留整数)
相关知识点
推荐套卷
如图13,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离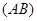 是1.7m,看旗杆顶部
是1.7m,看旗杆顶部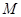 的仰角为
的仰角为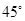 ;小红的眼睛与地面的距离
;小红的眼睛与地面的距离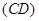 是1.5m,看旗杆顶部
是1.5m,看旗杆顶部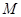 的仰角为
的仰角为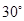 .两人相距28米且位于旗杆两侧(点
.两人相距28米且位于旗杆两侧(点 在同一条直线上).
在同一条直线上).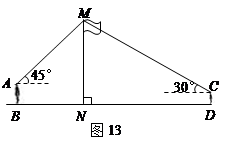
请求出旗杆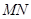 的高度.(参考数据:
的高度.(参考数据: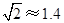 ,
,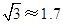 ,结果保留整数)
,结果保留整数)