问题提出
（1）如图①，在中，，，点关于所在直线的对称点为，则的长度为 ．
问题探究
（2）如图②，半圆的直径，是的中点，点在上，且，是上的动点，试求的最小值．
问题解决
（3）如图③，扇形花坛的半径为，．根据工程需要．现想在上选点，在边上选点，在边上选点，用装饰灯带在花坛内的地面上围成一个，使晚上点亮时，花坛中的花卉依然赏心悦目．为了既节省材料，又美观大方，需使得灯带的长度最短，并且用长度最短的灯带围成的为等腰三角形．试求的值最小时的等腰的面积．（安装损耗忽略不计）
（自贡）在△ABC中，AB=AC=5，cos∠ABC=
，将△ABC绕点C顺时针旋转，得到△A1B1C．
（1）如图①，当点B1在线段BA延长线上时．①求证：BB1∥CA1；②求△AB1C的面积；
（2）如图②，点E是BC边的中点，点F为线段AB上的动点，在△ABC绕点C顺时针旋转过程中，点F的对应点是F1，求线段EF1长度的最大值与最小值的差．
（南充）如图，矩形纸片ABCD，将△AMP和△BPQ分别沿PM和PQ折叠（AP＞AM），点A和点B都与点E重合；再将△CQD沿DQ折叠，点C落在线段EQ上点F处．
（1）判断△AMP，△BPQ，△CQD和△FDM中有哪几对相似三角形？（不需说明理由）
（2）如果AM=1，sin∠DMF=
，求AB的长．
（南充）如图，点P是正方形ABCD内一点，点P到点A、B和D的距离分别为1，
，
，△ADP沿点A旋转至△ABP′，连结PP′，并延长AP与BC相交于点Q．
（1）求证：△APP′是等腰直角三角形；
（2）求∠BPQ的大小；
（3）求CQ的长．
（南充）已知抛物线
与x轴交于点A（m﹣2，0）和B（2m+1，0）（点A在点B的左侧），与y轴相交于点C，顶点为P，对称轴为l：x=1．
（1）求抛物线解析式．
（2）直线
（
）与抛物线相交于两点M（
，
），N（
，
）（
），当
最小时，求抛物线与直线的交点M与N的坐标．
（3）首尾顺次连接点O、B、P、C构成多边形的周长为L，若线段OB在x轴上移动，求L最小值时点O，B移动后的坐标及L的最小值．
的解集，并把它们的解集在数轴上表示出来．
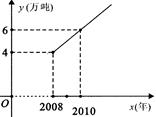
粤公网安备 44130202000953号