星期天,小强去水库大坝游玩,他站在大坝上的A处看到一棵大树的影子刚好落在坝底的B处(点A与大树及其影子在同一平面内),此时太阳光与地面成60 角.在A处测得树顶D的俯角为15
角.在A处测得树顶D的俯角为15 .如图所示,已知AB与地面的夹角为 60
.如图所示,已知AB与地面的夹角为 60 ,AB为8米.请你帮助小强计算一下这颗大树的高度? (结果精确到1米 .参考数据
,AB为8米.请你帮助小强计算一下这颗大树的高度? (结果精确到1米 .参考数据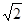 ≈1.4
≈1.4 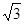 ≈1.7)
≈1.7)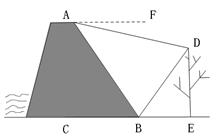
相关知识点
推荐套卷
星期天,小强去水库大坝游玩,他站在大坝上的A处看到一棵大树的影子刚好落在坝底的B处(点A与大树及其影子在同一平面内),此时太阳光与地面成60 角.在A处测得树顶D的俯角为15
角.在A处测得树顶D的俯角为15 .如图所示,已知AB与地面的夹角为 60
.如图所示,已知AB与地面的夹角为 60 ,AB为8米.请你帮助小强计算一下这颗大树的高度? (结果精确到1米 .参考数据
,AB为8米.请你帮助小强计算一下这颗大树的高度? (结果精确到1米 .参考数据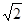 ≈1.4
≈1.4 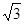 ≈1.7)
≈1.7)