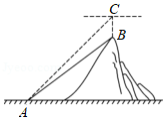
如图所示,某集团的项目组计划在山脚下点与山顶点之间修建一条索道,现利用无人机测算、两点间的距离.无人机飞至山顶点的正上方点处时,测得山脚下点的俯角约为,点与点的高度差为,,求山脚下点到山顶点的距离.
相关知识点
推荐套卷
如图所示,某集团的项目组计划在山脚下点与山顶点之间修建一条索道,现利用无人机测算、两点间的距离.无人机飞至山顶点的正上方点处时,测得山脚下点的俯角约为,点与点的高度差为,,求山脚下点到山顶点的距离.
