（本题10分）如图，P是双曲线
的一个分支上的一点，以点P为圆心，1个单位长度为半径作⊙P，设点P的坐标为（
，
）．
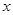（1）求当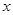为何值时，⊙P与直线
相切，并求点P的坐标．
（2）直接写出当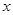为何值时，⊙P与直线相交、相离．
，其中
．
]
＋3
－
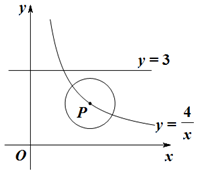
－0．25相关知识点
推荐套卷
（本题10分）如图，P是双曲线的一个分支上的一点，以点P为圆心，1个单位长度为半径作⊙P，设点P的坐标为（，）．
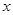（1）求当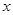为何值时，⊙P与直线相切，并求点P的坐标．
（2）直接写出当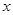为何值时，⊙P与直线相交、相离．
粤公网安备 44130202000953号