如图,一个点从数轴上的原点开始,先向左移动 到达
到达 点,再向左移动
点,再向左移动 到达
到达 点,然后向右移动
点,然后向右移动 到达
到达 点.
点.
(1)用1个单位长度表示 ,请你在数轴上表示出
,请你在数轴上表示出 、
、 、
、 三点的位置;
三点的位置;

(2)把点 到点
到点 的距离记为
的距离记为 ,则
,则 =
=  .
.
(3)阅读理解:观察式子: 因此可以得到:括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
因此可以得到:括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
问题解决
若点 以每秒
以每秒 的速度向左移动,同时
的速度向左移动,同时 、
、 点分别以每秒
点分别以每秒 、
、 的速度向右移动.设移动时间为
的速度向右移动.设移动时间为 秒,试探索:
秒,试探索: 的值是否会随着
的值是否会随着 的变化而改变?请说明理由.
的变化而改变?请说明理由.
推荐套卷
 ,画出△
,画出△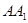 的长度;
的长度;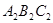 ,并写出△
,并写出△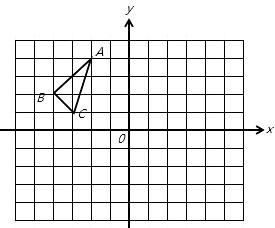


 粤公网安备 44130202000953号
粤公网安备 44130202000953号