如图，在△ABC中，∠BAC=90°，AB=6cm，BC=10cm，点D在线段AC上，且CD=2cm，动点P从BA的延长线上距A点10cm的E点出发，以每秒2cm的速度沿射线EA的方向运动了t秒．
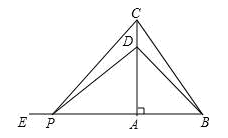
（1）求AD的长．
（2）直接写出用含有t的代数式表示PE= ．
（3）在运动过程中，是否存在某个时刻，使△ABC与△ADP全等？若存在，请求出t值；若不存在，请说明理由．
相关试题
某“爱心义卖”活动中，购进甲、乙两种文具，甲每个进货价高于乙进货价10元，90元买乙的数量与150元买甲的数量相同．
（1）求甲、乙进货价；
（2）甲、乙共100件，将进价提高20%进行销售，进货价少于2080元，销售额要大于2460元，求有几种方案？
关于体育选考项目统计图
| 项目 |
频数 |
频率 |
| A |
80 |
b |
| B |
c |
0．3 |
| C |
20 |
0．1 |
| D |
40 |
0．2 |
| 合计 |
a |
1 |
（1）求出表中a，b，c的值，并将条形统计图补充完整．
表中a=，b=，c=．
（2）如果有3万人参加体育选考，会有多少人选择篮球？
，在﹣2，0，1，2四个数中选一个合适的代入求值．如图，在△ABC中，AB=AC，AD⊥AB点D，BC=10cm，AD=8cm，点P从点B出发，在线段BC上以每秒3cm的速度向点C匀速运动，与此同时，垂直于AD的直线m从底边BC出发，以每秒2cm的速度沿DA方向匀速平移，分别交AB、AC、AD于E、F、H，当点P到达点C时，点P与直线m同时停止运动，设运动时间为t秒（t＞0）。
（1）当t=2时，连接DE、DF，求证：四边形AEDF为菱形；
（2）在整个运动过程中，所形成的△PEF的面积存在最大值，当△PEF的面积最大时，求线段BP的长；
（3）是否存在某一时刻t，使△PEF为直角三角形？若存在，请求出此时刻t的值，若不存在，请说明理由。
相关知识点
推荐套卷
粤公网安备 44130202000953号