如图,直角三角形ABC中,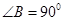 ,
,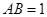 ,
,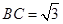 ,点M,N分别在边AB和AC上(M点和B点不重合),将
,点M,N分别在边AB和AC上(M点和B点不重合),将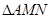 沿MN翻折,
沿MN翻折,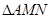 变为
变为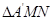 ,使顶点
,使顶点 落在边BC上(
落在边BC上( 点和B点不重合),设
点和B点不重合),设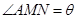 .
.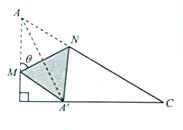
(1)用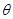 表示线段AM的长度,并写出
表示线段AM的长度,并写出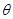 的取值范围;
的取值范围;
(2)求线段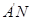 长度的最小值.
长度的最小值.
推荐套卷
如图,直角三角形ABC中,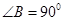 ,
,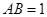 ,
,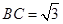 ,点M,N分别在边AB和AC上(M点和B点不重合),将
,点M,N分别在边AB和AC上(M点和B点不重合),将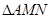 沿MN翻折,
沿MN翻折,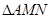 变为
变为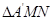 ,使顶点
,使顶点 落在边BC上(
落在边BC上( 点和B点不重合),设
点和B点不重合),设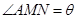 .
.
(1)用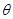 表示线段AM的长度,并写出
表示线段AM的长度,并写出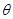 的取值范围;
的取值范围;
(2)求线段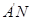 长度的最小值.
长度的最小值.