从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下图频率分布直方图: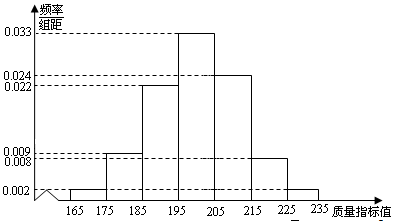
(Ⅰ)求这500件产品质量指标值的样本平均值 和样本方差
和样本方差 (同一组的数据用该组区间的中点值作代表);
(同一组的数据用该组区间的中点值作代表);
(Ⅱ)由直方图可以认为,这种产品的质量指标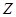 服从正态分布
服从正态分布 ,其中
,其中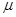 近似为样本平均数
近似为样本平均数 ,
, 近似为样本方差
近似为样本方差 .
.
(ⅰ)利用该正态分布,求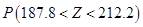 ;
;
(ⅱ)某用户从该企业购买了100件这种产品,记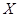 表示这100件产品中质量指标值位于区间
表示这100件产品中质量指标值位于区间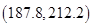 的产品件数.利用(ⅰ)的结果,求
的产品件数.利用(ⅰ)的结果,求 .
.
附: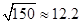 若
若 则
则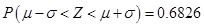 ,
,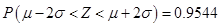 .
.
推荐套卷
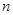 个首项都是1的等差数列,设第
个首项都是1的等差数列,设第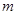 个数列的第
个数列的第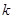 项为
项为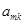
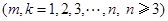 ,公差为
,公差为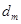 ,并且
,并且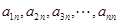 成等差数列.
成等差数列.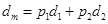 (
(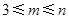 ,
,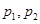 是
是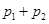 的值;
的值;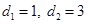 时,将数列
时,将数列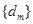 分组如下:
分组如下: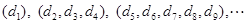 (每组数的个数构成等差数列).设前
(每组数的个数构成等差数列).设前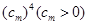 ,求数列
,求数列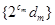 的前
的前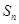 .
.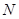 是不超过20的正整数,当
是不超过20的正整数,当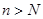 时,对于(Ⅱ)中的
时,对于(Ⅱ)中的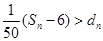 成立的所有
成立的所有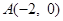 ,
, 为椭圆
为椭圆 的左、右顶点,
的左、右顶点,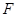 为其右焦点,
为其右焦点,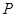 是椭圆
是椭圆 ,
,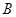 的动点,且
的动点,且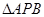 面积的最大值为
面积的最大值为 .
.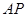 与椭圆在点
与椭圆在点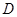 ,当直线
,当直线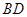 为直径的圆与直线
为直径的圆与直线 的位置关系,并加以证明.
的位置关系,并加以证明.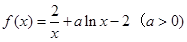 .
.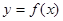 在点
在点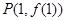 处的切线与直线
处的切线与直线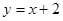 垂直,求函数
垂直,求函数 都有
都有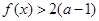 成立,试求
成立,试求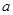 的取值范围;
的取值范围;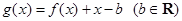 .当
.当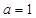 时,函数
时,函数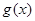 在区间
在区间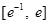 上有两个零点,求实数
上有两个零点,求实数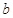 的取值范围.
的取值范围. .
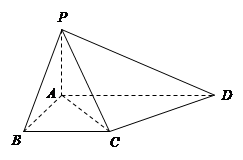
. 中,底面
中,底面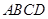 为直角梯形,且
为直角梯形,且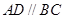 ,
,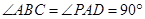 ,侧面
,侧面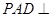 底面
底面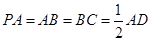 .
.
 平面
平面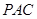 ;
;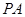 上是否存在点
上是否存在点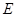 ,使得
,使得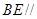 平面
平面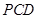 ?若存在,指出点
?若存在,指出点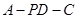 的余弦值.
的余弦值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号