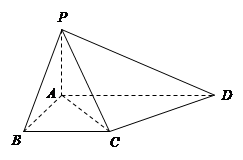
(本小题满分13分)如图,在四棱锥 中,底面
中,底面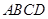 为直角梯形,且
为直角梯形,且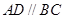 ,
,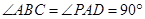 ,侧面
,侧面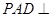 底面
底面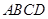 .若
.若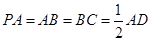 .
.
(Ⅰ)求证: 平面
平面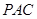 ;
;
(Ⅱ)侧棱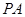 上是否存在点
上是否存在点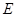 ,使得
,使得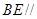 平面
平面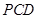 ?若存在,指出点
?若存在,指出点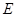 的位置并证明,若不存在,请说明理由;
的位置并证明,若不存在,请说明理由;
(Ⅲ)求二面角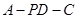 的余弦值.
的余弦值.
相关知识点
推荐套卷
(本小题满分13分)如图,在四棱锥 中,底面
中,底面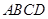 为直角梯形,且
为直角梯形,且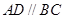 ,
,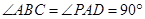 ,侧面
,侧面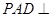 底面
底面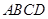 .若
.若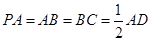 .
.
(Ⅰ)求证: 平面
平面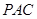 ;
;
(Ⅱ)侧棱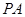 上是否存在点
上是否存在点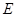 ,使得
,使得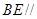 平面
平面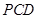 ?若存在,指出点
?若存在,指出点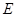 的位置并证明,若不存在,请说明理由;
的位置并证明,若不存在,请说明理由;
(Ⅲ)求二面角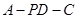 的余弦值.
的余弦值.