如图，AB是的⊙O直径，CB与⊙O相切于B，E为线段CB上一点，连接AC、AE分别交⊙O于D、G两点，连接DG交CB于点F．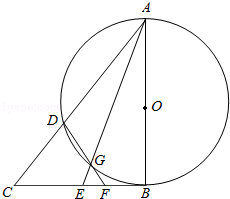
（Ⅰ）求证：C、D、G、E四点共圆．
（Ⅱ）若F为EB的三等分点且靠近E，EG=1，GA=3，求线段CE的长．
相关试题
与
，其中
，求
和
的值；
，求
的值域。
为合格品的概率为
（
1，2，3），设各次制造的零件合格与否是相互独立的，以
表示合格品的个数，求
为随机变量，求
是数列
的前
项和，
，
.
，求数列
的前
.推荐套卷
如图，AB是的⊙O直径，CB与⊙O相切于B，E为线段CB上一点，连接AC、AE分别交⊙O于D、G两点，连接DG交CB于点F．
（Ⅰ）求证：C、D、G、E四点共圆．
（Ⅱ）若F为EB的三等分点且靠近E，EG=1，GA=3，求线段CE的长．
粤公网安备 44130202000953号