设函数f(x)=lnx－ax+
－1.
(1) 当a=1时, 过原点的直线与函数f(x)的图象相切于点P, 求点P的坐标;
(2) 当0＜a＜
时, 求函数f(x)的单调区间；
(3) 当a=
时, 设函数g(x)=x2－2bx－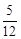
, 若对于
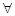x1∈
, 
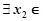[0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.（e是自然对数的底, e＜
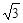+1）.
－
.
>0；
.
； (2)y＝lg(3－4sin2x)．
与sin
；相关知识点
推荐套卷
设函数f(x)=lnx－ax+－1.
(1) 当a=1时, 过原点的直线与函数f(x)的图象相切于点P, 求点P的坐标;
(2) 当0＜a＜时, 求函数f(x)的单调区间；
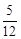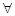(3) 当a=时, 设函数g(x)=x2－2bx－, 若对于x1∈, 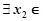[0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.（e是自然对数的底, e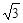＜+1）.
粤公网安备 44130202000953号