某网站用“10分制”调查一社区人们的幸福度.现从调查人群中随机抽取16名, 以下茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎, 小数点后的一位数字为叶):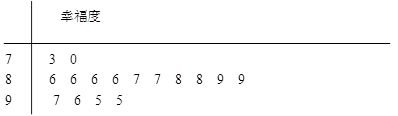
(1) 指出这组数据的众数和中位数;
(2) 若幸福度不低于9.5分, 则称该人的幸福度为“极幸福”.求从这16人中随机选取3人, 至多有1人是“极幸福”的概率;
(3) 以这16人的样本数据来估计整个社区的总体数据, 若从该社区(人数很多)任选3人, 记 表示抽到“极幸福”的人数, 求
表示抽到“极幸福”的人数, 求 的分布列及数学期望.
的分布列及数学期望.
推荐套卷
某网站用“10分制”调查一社区人们的幸福度.现从调查人群中随机抽取16名, 以下茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎, 小数点后的一位数字为叶):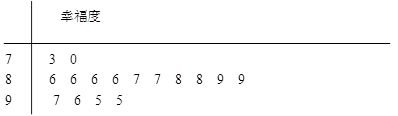
(1) 指出这组数据的众数和中位数;
(2) 若幸福度不低于9.5分, 则称该人的幸福度为“极幸福”.求从这16人中随机选取3人, 至多有1人是“极幸福”的概率;
(3) 以这16人的样本数据来估计整个社区的总体数据, 若从该社区(人数很多)任选3人, 记 表示抽到“极幸福”的人数, 求
表示抽到“极幸福”的人数, 求 的分布列及数学期望.
的分布列及数学期望.