如图，OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，求D、E两点的坐标．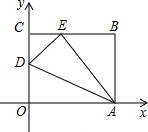
相关试题
∠BOC，∠COD=∠AOD=3∠AOB，求∠AOB和∠COD的度数．
AC，D、E分别为AC、AB的中点，求DE的长．
=
﹣1．
相关知识点
推荐套卷
如图，OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，求D、E两点的坐标．
粤公网安备 44130202000953号