一种长方形餐桌的四周可以坐6人用餐(带阴影的小长方形表示1个人的位置).现把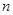 张这样的餐桌按如图方式拼接起来.
张这样的餐桌按如图方式拼接起来.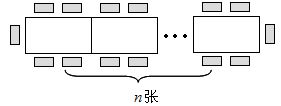
(1)问四周可以坐多少人用餐?(用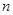 的代数式表示)
的代数式表示)
(2)若有26人用餐,至少需要多少张这样的餐桌?
相关知识点
推荐套卷
一种长方形餐桌的四周可以坐6人用餐(带阴影的小长方形表示1个人的位置).现把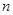 张这样的餐桌按如图方式拼接起来.
张这样的餐桌按如图方式拼接起来.
(1)问四周可以坐多少人用餐?(用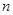 的代数式表示)
的代数式表示)
(2)若有26人用餐,至少需要多少张这样的餐桌?