如图,正方形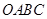 的面积为9,点
的面积为9,点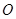 为坐标原点,点
为坐标原点,点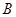 在函数
在函数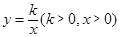 的图象上,点
的图象上,点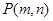 是函数
是函数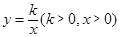 的图象上任意一点,边点
的图象上任意一点,边点 分别作
分别作 轴、
轴、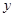 轴的垂线,垂足分别为
轴的垂线,垂足分别为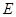 、
、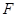 ,并设矩形
,并设矩形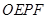 和正方形
和正方形 不重合部分的面积为S.
不重合部分的面积为S.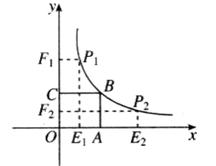
⑴求
 点的坐标和
点的坐标和 的值;
的值;⑵当
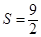 时,求
时,求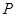 点的坐标;
点的坐标;⑶写出
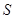 关于
关于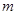 的函数关系式.
的函数关系式.
相关知识点
推荐套卷
如图,正方形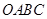 的面积为9,点
的面积为9,点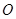 为坐标原点,点
为坐标原点,点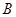 在函数
在函数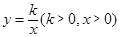 的图象上,点
的图象上,点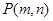 是函数
是函数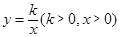 的图象上任意一点,边点
的图象上任意一点,边点 分别作
分别作 轴、
轴、 轴的垂线,垂足分别为
轴的垂线,垂足分别为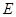 、
、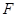 ,并设矩形
,并设矩形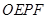 和正方形
和正方形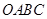 不重合部分的面积为S.
不重合部分的面积为S.
⑴求
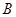 点的坐标和
点的坐标和 的值;
的值;⑵当
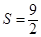 时,求
时,求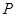 点的坐标;
点的坐标;⑶写出
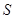 关于
关于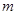 的函数关系式.
的函数关系式.