（本题6分）下列图形是否是轴对称图形，画出轴对称图形的所有对称轴．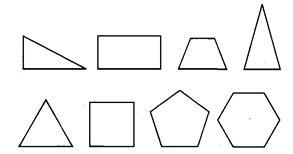
思考：正三角形有_______条对称轴；正四边形有______条对称轴；正五边形有_______条对称轴；正六边形有_______条对称轴；正n边形有_______条对称轴．
当n越来越大时，正多边形接近于什么图形？它有多少条对称轴？
；
，并将其解集表示在数轴上．
，其中
．
．
．
．相关知识点
推荐套卷
（本题6分）下列图形是否是轴对称图形，画出轴对称图形的所有对称轴．
思考：正三角形有_______条对称轴；正四边形有______条对称轴；正五边形有_______条对称轴；正六边形有_______条对称轴；正n边形有_______条对称轴．
当n越来越大时，正多边形接近于什么图形？它有多少条对称轴？
粤公网安备 44130202000953号