如图，在12×12的正方形网格中，△TAB的顶点分别为T（1,1），A（2,3），B（4,2）。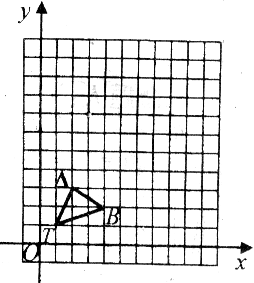
（1）以点T（1,1）为位似中心，按比例尺（TA′：TA）3:1的位似中心的同侧将TAB放大为△TA′B′，放大后点A，B的对应点分别为A′，B′，画出△TA′B′，并写出点A′，B′的坐标；
（2）在（1）中，若C（a，b）为线段AB上任一点，写出变化后点C的对应点C′的坐标。
可以被10和20之间某两个数整除，求这两个数
，求
的值？
；
；
；
；推荐套卷
如图，在12×12的正方形网格中，△TAB的顶点分别为T（1,1），A（2,3），B（4,2）。
（1）以点T（1,1）为位似中心，按比例尺（TA′：TA）3:1的位似中心的同侧将TAB放大为△TA′B′，放大后点A，B的对应点分别为A′，B′，画出△TA′B′，并写出点A′，B′的坐标；
（2）在（1）中，若C（a，b）为线段AB上任一点，写出变化后点C的对应点C′的坐标。
粤公网安备 44130202000953号